@
目录- 1、二叉搜索树
- 1.1、 基本概念
- 1.2、树的节点(BinaryNode)
- 1.3、构造器和成员变量
- 1.3、公共方法(public method)
- 1.4、比较函数
- 1.5、contains 函数
- 1.6、findMin
- 1.7、findMax
- 1.8、insert
- 1.9、remove
- 二、完整代码实现(Java)
1、二叉搜索树
1.1、 基本概念
二叉树的一个性质是一棵平均二叉树的深度要比节点个数N小得多。分析表明其平均深度为\(\mathcal{O}(\sqrt{N})\),而对于特殊类型的二叉树,即二叉查找树(binary search tree),其深度的平均值为\(\mathcal{O}(log N)\)。
二叉查找树的性质: 对于树中的每个节点X,它的左子树中所有项的值小于X中的项,而它的右子树中所有项的值大于X中的项。
由于树的递归定义,通常是递归地编写那些操作的例程。因为二叉查找树的平均深度为\(\mathcal{O}(log N)\),所以一般不必担心栈空间被用尽。
1.2、树的节点(BinaryNode)
二叉查找树要求所有的项都能够排序,有两种实现方式;
- 对象实现接口 Comparable, 树中的两项使用compareTo方法进行比较;
- 使用一个函数对象,在构造器中传入一个比较器;
本篇文章采用了构造器重载,并定义了myCompare方法,使用了泛型,因此两种方式都支持,在后续的代码实现中可以看到。
节点定义:
/** * 节点 * * @param <AnyType> */ private static class BinaryNode<AnyType> { BinaryNode(AnyType theElement) { this(theElement, null, null); } BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right) { element = theElement; left = left; right = right; } AnyType element; // the data in the node BinaryNode<AnyType> left; // Left child BinaryNode<AnyType> right; // Right child }1.3、构造器和成员变量
private BinaryNode<AnyType> root; private Comparator<? super AnyType> cmp; /** * 无参构造器 */ public BinarySearchTree() { this(null); } /** * 带参构造器,比较器 * * @param c 比较器 */ public BinarySearchTree(Comparator<? super AnyType> c) { root = null; cmp = c; }关于比较器的知识可以参考下面这篇文章:
Java中Comparator的使用
关于泛型的知识可以参考下面这篇文章:
如何理解 Java 中的 <T extends Comparable<? super T>>
1.3、公共方法(public method)
主要包括插入,删除,找到最大值、最小值,清空树,查看元素是否包含;
/** * 清空树 */ public void makeEmpty() { root = null; } public boolean isEmpty() { return root == null; } public boolean contains(AnyType x){ return contains(x,root); } public AnyType findMin(){ if (isEmpty()) throw new BufferUnderflowException(); return findMin(root).element; } public AnyType findMax(){ if (isEmpty()) throw new BufferUnderflowException(); return findMax(root).element; } public void insert(AnyType x){ root = insert(x, root); } public void remove(AnyType x){ root = remove(x,root); }1.4、比较函数
如果有比较器,就使用比较器,否则要求对象实现了Comparable接口;
private int myCompare(AnyType lhs, AnyType rhs) { if (cmp != null) { return cmp.compare(lhs, rhs); } else { return lhs.compareTo(rhs); } }1.5、contains 函数
本质就是一个树的遍历;
private boolean contains(AnyType x, BinaryNode<AnyType> t) { if (t == null) { return false; } int compareResult = myCompare(x, t.element); if (compareResult < 0) { return contains(x, t.left); } else if (compareResult > 0) { return contains(x, t.right); } else { return true; } }1.6、findMin
因为二叉搜索树的性质,最小值一定是树的最左节点,要注意树为空的情况。
/** * Internal method to find the smallest item in a subtree * @param t the node that roots the subtree * @return node containing the smallest item */ private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) { if (t == null) { return null; } if (t.left == null) { return t; } return findMin(t.left); }1.7、findMax
最右节点;
/** * Internal method to find the largest item in a subtree * @param t the node that roots the subtree * @return the node containing the largest item */ private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t){ if (t == null){ return null; } if (t.right == null){ return t; } return findMax(t.right); }1.8、insert
这个主要是根据二叉搜索树的性质,注意当树为空的情况,就可以加入新的节点了,还有当该值已经存在时,默认不进行操作;
/** * Internal method to insert into a subtree * @param x the item to insert * @param t the node that roots the subtree * @return the new root of the subtree */ private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){ if (t == null){ return new BinaryNode<>(x,null,null); } int compareResult = myCompare(x,t.element); if (compareResult < 0){ t.left = insert(x,t.left); } else if (compareResult > 0){ t.right = insert(x,t.right); } else{ //Duplicate; do nothing } return t; }1.9、remove

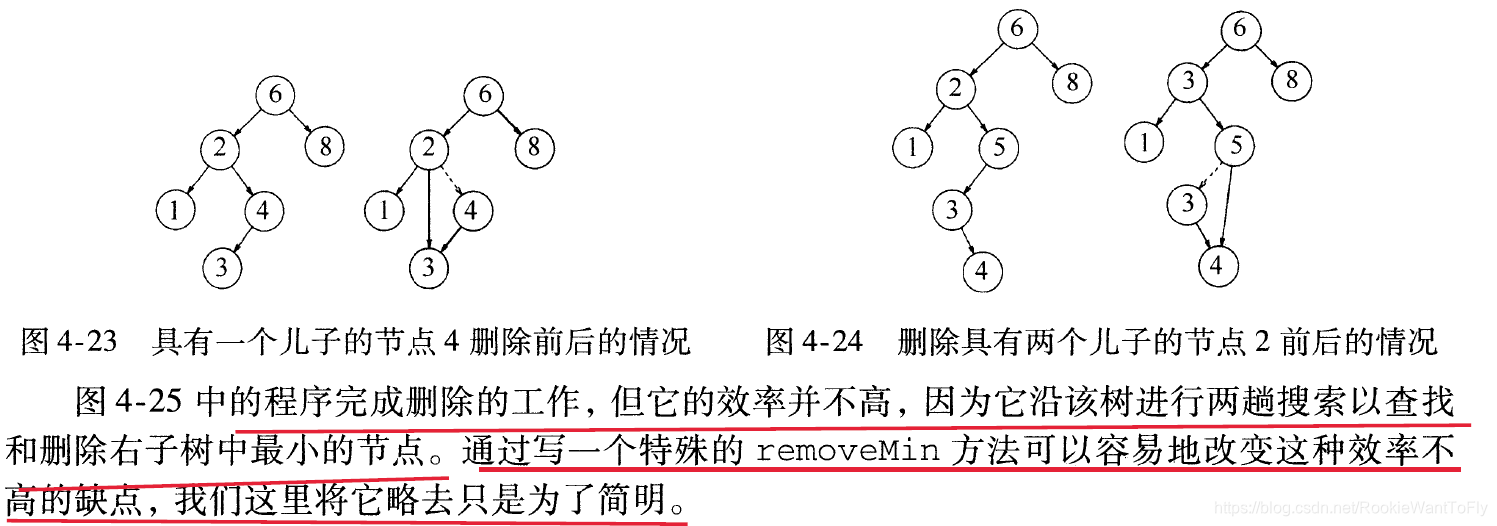

注意当空树时,返回null;
最后一个三元表达式,是在之前已经排除掉节点有两个儿子的情况下使用的。
/** * Internal method to remove from a subtree * @param x the item to remove * @param t the node that roots the subtree * @return the new root of the subtree */ private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t){ if (t == null){ return t; // Item not found ,do nothing } int compareResult = myCompare(x,t.element); if (compareResult < 0){ t.left = remove(x,t.left); } else if (compareResult > 0){ t.right = remove(x,t.right); } else if (t.left !=null && t.right!=null){ //Two children t.element = findMin(t.right).element; t.right = remove(t.element,t.right); } else t = (t.left !=null) ? t.left:t.right; return t; }二、完整代码实现(Java)
/** * @author LongRookie * @description: 二叉搜索树 * @date 2021/6/26 19:41 */import com.sun.source.tree.BinaryTree;import java.nio.BufferUnderflowException;import java.util.Comparator;/** * 二叉搜索树 */public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> { /** * 节点 * * @param <AnyType> */ private static class BinaryNode<AnyType> { BinaryNode(AnyType theElement) { this(theElement, null, null); } BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right) { element = theElement; left = left; right = right; } AnyType element; // the data in the node BinaryNode<AnyType> left; // Left child BinaryNode<AnyType> right; // Right child } private BinaryNode<AnyType> root; private Comparator<? super AnyType> cmp; /** * 无参构造器 */ public BinarySearchTree() { this(null); } /** * 带参构造器,比较器 * * @param c 比较器 */ public BinarySearchTree(Comparator<? super AnyType> c) { root = null; cmp = c; } /** * 清空树 */ public void makeEmpty() { root = null; } public boolean isEmpty() { return root == null; } public boolean contains(AnyType x){ return contains(x,root); } public AnyType findMin(){ if (isEmpty()) throw new BufferUnderflowException(); return findMin(root).element; } public AnyType findMax(){ if (isEmpty()) throw new BufferUnderflowException(); return findMax(root).element; } p......原文转载:http://www.shaoqun.com/a/852299.html
跨境电商:https://www.ikjzd.com/
新单:https://www.ikjzd.com/w/79
亚马逊t恤:https://www.ikjzd.com/w/1932
costco:https://www.ikjzd.com/w/1680
@目录1、二叉搜索树1.1、基本概念1.2、树的节点(BinaryNode)1.3、构造器和成员变量1.3、公共方法(publicmethod)1.4、比较函数1.5、contains函数1.6、findMin1.7、findMax1.8、insert1.9、remove二、完整代码实现(Java)1、二叉搜索树1.1、基本概念二叉树的一个性质是一棵平均二叉树的深度要比节点个数N小得多。分析表明其
亚马逊站内广告如何创建?(附图文实操详解):https://www.ikjzd.com/articles/104239
国务院:2019年底前出台对跨境电商等企业的认证标准!:https://www.ikjzd.com/articles/104240
想提升亚马逊listing转化率,这些数据你每天都要看!:https://www.ikjzd.com/articles/104241
速卖通店铺流量下滑原因有哪些,如何对症下药?:https://www.ikjzd.com/articles/104243
三个黑人玩一个少妇 两个男人一个前面一个后面:http://lady.shaoqun.com/a/247877.html
换妻游戏没能给我带来难忘的快感(3/3):http://lady.shaoqun.com/a/66904.html
女生喊痛男生还继续塞 女人越喊痛男人越用力冲刺:http://lady.shaoqun.com/m/a/247502.html
女人最喜欢被㖭的是地方 喜欢让同学㖭我下面的感觉:http://lady.shaoqun.com/m/a/248367.html
词缀en的常见意义和用法:http://lady.shaoqun.com/a/405834.html
2021深圳锦绣中华民俗村泼水节夜场攻略:http://www.30bags.com/a/476661.html
活一次多久正常?:http://lady.shaoqun.com/a/406828.html
"父母无法发现的瞬间":http://lady.shaoqun.com/a/406829.html
No comments:
Post a Comment